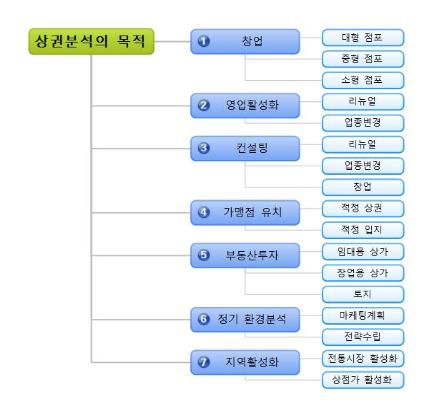
자본비용(Cost of Capital)과 Systematic Risk


자본비용(Cost of Capital)과 Systematic Risk
베타(β: Beta), Systematic Risk, Unsystematic Risk, Total Risk
 

CAPM(Capital Asset Pricing Model)은 적절한 할인율(Discount Rate), 즉 적절한 자본비용을 계산하는 방법을 제시하고 있다고 한다. 그런데, 적절하다는 것은 무엇에 대해 적절하다는 것인가? 그것은 위험 수준(Risk)을 고려했을 때 적절하다는 것이다. 그러니까, 주식(또는 프로젝트, 기업 등)의 위험성을 고려했을 때, 그 정도의 할인율이라면 적절한 보상이 이루어진 것이라는 의미이다.

 

Total Risk = Systematic Risk + Unsystematic Risk


     i라는 주식이 있다고 하고, 이 주식의 수익률을 Ri로 표시했을 때, 포트폴리오(Portfolio) 이론에서는 투자자들이 이러한 주식의 위험성(Risk)을 Ri의 표준편차(Standard Deviation)로 측정한다고 가정했다. 통계학에서 표준편차의 “정의”가 분산(Variance)의 1/2 제곱이기 때문에, 위험성의 지표로 표준편차 대신 분산을 사용해도 결론은 같아지는데, 분산을 사용하는 것이 위험성을 설명하는 데 더 편리한 경우가 많기 때문에 흔히 분산을 사용해서 위험성을 정의하고 설명하는 경우가 많다.


     따라서 주식 i의 위험성(Risk)을 포트폴리오 이론에 따라 Ri의 Variance(분산), 즉 Var(Ri)라고 정의(Define)해 보자. 그리고 앞에서 설명한 one-Index Model이 다음과 같은 관계를 가정(Assume)하고 있음을 생각해 보자.



     Ri  =  αi + βiRm + ei               (1)



그러면 주식 i의 위험성, 즉 Var(Ri)는 다음과 같이 된다.


     Var(Ri) = (βi)2 Var(Rm) + Var(ei)        (3)



여기서 Ri의 분산, 즉 Var(Ri)가 위의 (3)과 같이 되는 이유는 Rm과 ei 사이에 아무 관계가 없다고 “가정하기 때문”이다, 즉 Rm과 ei의 공분산(Covariance)이 영(Zero)이라고 가정하기 때문이다. (통계학에서 분산과 공분산을 아직 안 배웠거나 잘 모른다면, 몇 가지 가정 아래서 위 (3)과 같은 관계가 성립한다는 정도로 이해하고 그냥 넘어가도 괜찮다, 박사 과정을 하는 게 아니라면 - - -)


     위의 (3)은 주식 i의 위험성 전체(Total Risk)를 두 부분으로 나누어 생각할 수 있음을 보여 주고 있다. 즉, 주식 i의 위험성 전체인 Var(Ri)가  (βi)2 Var(Rm)와  Var(ei),  두 부분으로 구성되어 있음을 보여 주고 있는데, 위 (3)의 각 부분에 대해 다음과 같은 용어를 사용한다.



     Var(Ri) :  Total Risk
     (βi)2 Var(Rm) :  Systematic Risk 또는 Undiversifiable Risk 또는 Market Risk
     Var(ei) :  Unsystematic Risk 또는 Diversifiable Risk 또는 Firm-specific Risk



Total Risk는 위험성 전체를 의미하는데, 이 가운데 시장 전반의 구조적 요인으로 인해 영향받게 되는 위험성 부분을 “Systematic Risk”, 즉 “시장 구조적 위험성”이라 하고(우리말로 “체계적 위험”이라는 용어를 많이 쓰는데, 선뜻 이해하기에 좋은 용어는 아니다), 시장 상황과 무관한 개별 기업 특유의 요인으로 인해 발생하는 위험성 부분을 “Unsystematic Risk”, 즉 “시장 구조와 무관한 위험성”이라 한다.



     Systematic Risk는 포트폴리오를 구성하여 다양한 주식에 분산 투자를 한다 하더라도 제거할 수가 없다는 의미에서 “Undiversifiable Risk”, 즉 “분산이 가능하지 않은 위험성”이라고도 하고, 또 시장 상황 때문에 발생하는 위험성이라는 의미에서 간단히 “Market Risk”, 즉 “시장 위험성”이라고도 한다. 반면에 Unsystematic Risk는 포트폴리오를 구성해서 분산 투자를 함으로써 제거가 가능한 위험성이라는 의미에서 “Diversifiable Risk”, 즉 “분산이 가능한 위험성”이라고도 하고, 개별 기업 특유의 성격으로 인한 위험성이라는 의미에서 “Firm-specific Risk”, 즉 “기업 특유의 위험성”이라고도 한다.



     포트폴리오 이론에 의하면, 다양한 종류의 주식으로 포트폴리오를 구성할 때, 개별 주식들의 Unsystematic Risk는 서로 상쇄되어 영에 가깝게 되고, Systematic Risk 부분만 남게 된다고 하는데, 이러한 사실은 포트폴리오 수익률의 Variance를 수리적으로 도출함으로써 입증할 수 있다. (그리 어려운 것은 아니나, 여기서도 전체 수리적 도출 과정은 생략하기로 하고, 참고로 일부 핵심적 부분만을 설명하면 다음과 같다.)




포트폴리오(Portfolio) 투자를 하면 Unsystematic Risk를 거의 영으로 만들 수 있다.



     위의 식 (1)과 (3)에서, 개별 주식 i에 대한 수익률 Ri 대신, 포트폴리오 전체에 대한 수익률을 Rp로, 포트폴리오 전체 수익률에 대한 베타를 βp로, 포트폴리오에 포함된 개별 주식 ei 의 합계를 ep 로 표시하면, 포트폴리오의 수익률은 다음과 같이 표시된다.



     Rp  =  αp + βpRm + ep               (4)



위의 식 (4)를 이용해서, (3)의 경우보다는 조금 복잡한 과정을 거쳐 포트폴리오 수익률의 Variance, 즉 Var(Rp)를 도출해 보면, 포트폴리오에 포함된 주식 수가 증가함에 따라 ep 부분은 무시해도 괜찮을 정도로 작아지고 βpRm 부분만 남게 됨을 보일 수 있다. 이는 무엇을 의미하는가?




자본비용을 결정하는 것은 Total Risk가 아니라 Systematic Risk다.


     포트폴리오 투자를 하는 투자자들의 입장에서 보면, 개별 주식의 리스크에 대해 합당한 보상(즉 합당한 수익률)을 요구할 때, 개별 주식(즉 기업) 특유의 성격으로 인해 발생하는 리스크에 대해서는 보상을 요구할 필요가 없다는 것이다, 시장 전체 상황과 연관된 리스크 부분에 대해서 만 보상을 요구하면 된다는 것이다. 다시 말해, Unsystematic Risk에 대해서는 보상(즉 수익률)을 요구할 필요가 없고, Systematic Risk에 대해서만 보상을 요구하면 된다는 의미로, 투자자들이 보상을 요구해야 하는 부분은 리스크 전체(Total Risk)에 대해서가 아니라 Systematic Risk 부분에 대해서 만이라는 것이다. 그리고 이러한 Systematic Risk가 어느 정도인지를 측정하는 도구가 베타(β: Beta)인 것이다. 



     이를 자본의 수요자인 기업의 입장에서 보면, 기업이 지불하게 되는 자본비용은 기업의 Total Risk가 아니라 Systematic Risk 부분에 의해서 결정된다는 것을 의미한다. 따라서 특정 주식(즉 기업)의 수익률 변동폭이 커서 주식 자체의 위험성은 높다 하더라도(즉 Total Risk인 Variance가 크다 하더라도), 이러한 수익률의 변동이 시장 전반의 수익률 변동과 별로 연관성이 없다면(즉 Systematic Risk가 크지 않다면), 투자자들 입장에서의 위험성은 그리 높은 것이 아니기 때문에 (즉 Systematic Risk의 측정치인 베타 값이 크지 않기 때문에) 요구 수익률을 높게 책정할 필요가 없고, 이는 기업 입장에서 자본비용이 높아지지 않는다는 것을 의미한다. 이것이 포트폴리오 이론에서 발전해 나간 CAPM과 one-Index Model이 자본비용의 결정에 대해 설명하는 핵심 내용이라 할 수 있다.
 

출처 : http://sunho55.blogspot.kr/2014/


저작자표시 비영리 변경금지

'鑑定評價理論 및 업역 확장 > 부동산 투자론' 카테고리의 다른 글

Capital Asset Pricing Model (CAPM): 베타(β: Beta)란? (III)개별 주식과 시장 전체의 연관성을 측정하는 지표다.  (0) 2017.05.14
Capital Asset Pricing Model (CAPM)이란? (II) (출처 : 최선호 교수 블로그)  (0) 2017.05.13
Capital Asset Pricing Model (CAPM)이란? (I) (출처 : 최선호 교수 블로그)  (0) 2017.05.12
임대주택사업의 사업성 분석방법 개선에 관한 연구 (유선종 교수님 외)  (0) 2015.09.26
상권분석 방법론 (출처 : 이데일리)  (0) 2015.09.16

Capital Asset Pricing Model (CAPM): 베타(β: Beta)란? (III)개별 주식과 시장 전체의 연관성을 측정하는 지표다.

CAPM에서, 우리가 베타의 정의(definition)를 보고 그 뜻을 바로 이해하기는 쉽지 않다. Cov(Ri,Rm)/σ2(Rm)라고 정의(define)된 베타를 왜 Ri(주식 i의 수익률, 즉 주식 i)와 Rm(시장 전체의 수익률, 즉 시장 전체)의 연관성을 측정하는 지표라고 하는 것일까?


 


베타는 선형 회귀분석(Linear Regression)에서 직선의 기울기를 나타내는 계수(Coefficient)다, 즉 Ri와 Rm의 선형(Linear: 직선) 관계를 나타내는 계수다.



    

포트폴리오(Portfolio) 이론은 투자자들이 예상 수익률(Expected Rate of Return)과 예상 수익률의 표준편차(Standard Deviation)를 사용해서 수익성(Return)과 리스크(Risk)을 판단한다고 가정하고 있고, 이러한 가정(Assumption) 아래서는 하나의 자산에만 투자하는 것보다 여러 개의 자산으로 구성된 포트폴리오에
투자하는 것이 리스크 대비 보다 높은 수익률을 올릴 수 있다는 것을 보여 주고 있다. 따라서 포트폴리오 투자를 하는 것이 합리적이고, 합리적인 투자자들이라면 리스크 대비 수익률을 최대화 할 수 있는 포트폴리오에 투자할 것이다. 그리고 이러한 투자 활동의 결과로 자산의 시장가격이 형성될 것이다.



     여기에 각 자산의 시장가격(또는 수익률)은 두 가지 요인에 의해 결정된다고 “가정해 보자”: 하나는 시장 전체의 좋고 나쁨, 즉 경기의 좋고 나쁨이라는 요인이고, 다른 하나는 시장과는 상관 없는 개별 기업(즉 자산) 특유의 경영 능력, 제품에 대한 수요 등의 요인에 의해 시장가격, 즉 수익률이 결정된다고 보는 것이다. 이를 수식으로 표현하면 다음과 같이 된다.



     Ri  =  αi + βiRm + ei               (1)


     여기서 Rm은 시장 전체적 요인을, ei는 개별 기업적 요인을 의미.


이 경우에, 포트폴리오 투자를 하게 되면, 개별 기업 특유의 요인으로 인한 부분, 즉 ei는 서로 상쇄되어 없어질 수 있다. 물론 그렇게 되려면 주식시장의 규모도 크고 또 충분히 성숙된 시장이어야 하지만, 일단 그렇다고 “가정하면”, 즉 E(ei) = 0라고 가정하면, 수식 (1)의 예상값(Expected Value 또는 기댓값)은 다음과 같이 된다.



     E(Ri) =  αi + βi E(Rm)               (2)


위 수식 (2)를 말로 설명하면, 주식 i의 예상 수익률은 시장 전체의 예상 수익률에 βi를 곱한 값에 상수 αi를 더한 값이라는 것인데, αi는 상수, 즉 변하지 않는 값이니까, 예상 시장수익률 E(Rm)이 경기 상황에 따라 결정되고 나면 주식 i의 예상 수익률은 βi에 의해 결정된다는 이야기가 된다. 위의 식 (1)과 (2) 같은 Ri와 Rm 사이의 관계를 선형 관계(Linear Relationship)라 하고, (1)과 (2) 같은 관계를 가정하고 αi와 βi의 값을 계산하는 것을 회귀분석(Regression Analysis)이라 한다. 이때 βi는 Ri와 Rm 사이에 형성되는 직선의 기울기가 된다, 즉 Ri와 Rm의 직선적 관계를 설명해 주는 계수인 것이다.



     여기서 CAPM을 생각해 보자. CAPM에 의하면 E(Ri) 값에 대해 E(Ri) = Rf + βi {E(Rm) - Rf} 라는 관계가 성립된다. 그런데 수식 (2)에 의하면 E(Ri) =  αi + βi E(Rm) 라는 관계가 성립된다. 그렇다면 CAPM에서의 베타(βi)와 수식 (2)에서의 베타(βi)는 같은 것인가? 그렇다, 수학적으로 정확하게 일치한다.


수식 (2)에서의 베타 값, 즉 직선 관계의 기울기를 구하는 공식은 Cov(Ri,Rm)/σ2(Rm) 으로, CAPM에서 베타의 정의와 정확하게 일치한다. 그러니까 CAPM에서 정의된 베타는, Ri와 Rm이 선형(직선) 관계를 갖고 있다고 가정했을 때, 그 직선 관계의 기울기에 해당하는 것이다, 즉 Ri와 Rm의 직접적(직선적) 관계를 나타내는 수치로, 개별 주식 i와 시장 전체의 연관성을 측정하는 수치가 되는 것이다.




One-Index Model, Multi-Index Model



     우리는 포트폴리오 이론을 이용해 E(Ri) = Rf + βi {E(Rm) - Rf} 이라는 CAPM을 개발했다, 즉 주식 i의 예상 수익률인 E(Ri)를 구하기 위해 CAPM을 사용한 것이다. 그런데 E(Ri)는 수식 (2)를 통해서도 구할 수 있다.


수식 (2)에 의하면 E(Ri)는 한 개의 독립변수(Independent Variable)인 E(Rm)에 의해 결정되기 때문에 수식 (2) 와 같은 모델을, CAPM과 구분하여, one-Index Model 또는 one-Factor Model이라고 한다. 수식 (2)에서 독립변수가 E(Rm), 시장 수익률이기 때문에 수식 (2)를 Market Model이라고 하기도 한다.



     결국 CAPM도 한 개의 독립변수 E(Rm)만을 사용하기 때문에 one-factor model이라 할 수 있다. 여기에서, E(Ri)가 반드시 한 개의 변수에 의해서만 결정된다고 볼 수는 없지 않느냐는 생각이 자연스럽게 나오게 되면서, E(Rm) 이외의 새로운 변수들을 찾아서 추가하는 Multi-factor model이 나오게 된다.
 


출처 : http://sunho55.blogspot.kr/2014/

저작자표시 비영리 변경금지

'鑑定評價理論 및 업역 확장 > 부동산 투자론' 카테고리의 다른 글

자본비용(Cost of Capital)과 Systematic Risk (체계적 위험)  (0) 2017.05.16
Capital Asset Pricing Model (CAPM)이란? (II) (출처 : 최선호 교수 블로그)  (0) 2017.05.13
Capital Asset Pricing Model (CAPM)이란? (I) (출처 : 최선호 교수 블로그)  (0) 2017.05.12
임대주택사업의 사업성 분석방법 개선에 관한 연구 (유선종 교수님 외)  (0) 2015.09.26
상권분석 방법론 (출처 : 이데일리)  (0) 2015.09.16



Capital Asset Pricing Model (CAPM)이란? (II)


Capital Asset Pricing Model (CAPM)이란? (II)
CAPM은 할인율을 어떻게 계산하고, 어떤 의미로 보고 있나?

앞에서 설명했던 것처럼, CAPM은 할인율(Discount Rate)을 계산해 내는 모델이다. 그런데 할인율이라는 용어는 경우에 따라 여러가지 다른 형태로 쓰인다. 예를 들어, 예상 수익률(Expected Rate of Return)이라고 하기도 하고, 요구 수익률(Required Rate of Return), 기회비용(Opportunity Cost), 자본비용(Cost of Capital) 등, 경우에 따라 다양한 용어로 불리운다. 문맥에 따라 이처럼 다양하게 불리우지만, 기본적으로 다 같은 개념이다. CAPM은 이러한 할인율을 어떻게 계산해 내고, 그 의미는 무엇인가?

 


CAPM: E(Ri) = Rf + βi {E(Rm) - Rf}
     CAPM은 위의 식으로 요약할 수 있다. 여기서
     E(Ri)는 i라는 주식(capital asset으로 주식만을 의미하는 것은 아니지만, 이해의 편의상, 간단히 주식이라 하자)에 투자했을 때 예상되는 수익률(Expected rate of return on security i)을 의미하고 (i에 특별한 의미는 없다, 그냥 하나의 주식을 의미한다),
     Rf는 Risk-free rate, 그러니까 투자에 따르는 위험이 전혀 없는, 무위험 자산에 투자했을 때의 수익률을 의미하며,
     E(Rm)은 시장에 존재하는 모든 자산들을 적절히 포함시켜 포트폴리오를 구성했을 때 예상되는 수익률로, 이렇게 구성된 포트폴리오를 Market Portfolio라 한다. 그러니까 E(Rm)은 시장 전체의 평균 수익률, 또는 시장 전체의 예상 수익률이라 할 수 있으며,
     βi는 베타(Beta) i라고 읽고, i라는 주식의 예상 수익률과 시장 전체의 예상 수익률 사이의 상관관계를 말한다.
     CAPM을 위와 같은 수학적 기호가 아닌, 말로 풀어서 쓰면 다음과 같이 된다;
     Expected Rate of Return
     = Risk-free Rate + β {Expected Market Return – Risk-free Rate}.
이를 좀 더 단순화 하면 다음과 같이 된다;
     Expected Rate of Return = Risk-free Rate + Risk Premium.
말하자면 주식은 무위험 자산이 아니기 때문에, 이처럼 위험이 따르는 자산에 투자할 때는 위험 정도에 따라 무위험 자산에 투자할 때보다 수익률을 더 요구해야 한다는 것이다. 그러니까, 먼저 Risk-free rate, 즉 무위험 자산에 투자했을 때 얻을 수 있는 수익률을 기본적으로 요구하고, 여기에 추가해서 위험 정도에 따라 수익률을 더 요구해야 한다는 것인데, 이때 위험 정도에 따라 추가로 요구하는 수익률을 “리스크 프리미엄(Risk Premium)”이라 한다. 사실 이 정도야 상식적인 이야기라 할 수 있지만, CAPM의 뛰어난 점은 이러한 리스크 프리미엄을 계산하는 방법을 이론적으로 제시했다는 데에 있다, 즉 Risk Premium = β {Expected Market Return – Risk-free Rate} 라는 관계를 이론적으로 도출해 냈다는 점이다.
     여기서 시장 전체의 예상 수익률과 무위험 자산에 대한 수익률의 차이, 즉 (Expected Market Return – Risk-free Rate)을 “Market risk premium (또는 Risk premium on the market)”이라고 한다. 이를 우리말로 번역한다면 “시장 전반에 대한 리스크 프리미엄”이라 할 수 있다. 그리고 베타(β: Beta)는 주식 i와 시장 전체와의 상관관계를 나타내는 수치로서 다음과 같이 정의(define)된다:

 


이때 Cov(Ri,Rm)은 개별 주식i와 시장과의 상관관계를 나타내는 Covariance(공분산)이고 σ2(Rm)은 시장 수익률의 Variance(분산)을 나타낸다. (Variance와 Covariance라는 통계학 개념에 대해 아직 배우지 않았다면 베타의 정의를 굳이 이해하지 않아도 된다.)

CAPM과 베타는 세 가지 가정(Assumption) 아래서 이론적으로 도출된다.
     CAPM은 세 가지 가정(Assumption) 아래 이론적으로 도출된 모델이다. 첫번째 가정은, 투자자들은 투자의 수익성을 판단하는 데 예상 수익률(Expected Rate of Return)을 사용하고, 투자의 리스크를 판단하는 데는 이러한 예상 수익률의 표준편차(Standard Deviation)를 사용해서 투자자산의 포트폴리오(Portfolio)를 구성한다는 것이다. 이러한 첫번째 가정은 Harry Markowitz가 1950년대 개발한 Portfolio 이론의 가장 기본적인 가정이기도 한데, CAPM은 Portfolio 이론을 Asset Pricing에 적용하면서 개발된 이론이라 할 수 있다. 만약 우리가 예상 수익률보다 더 좋은 수익성 지표를 생각해 내거나, 예상 수익률의 표준편차보다 더 좋은 리스크 지표를 생각해 낸다면, CAPM과는 다른, 더 발전된 새로운 Pricing Model을 개발할 수 있을 것이다.
     두번째 가정은 무위험 자산(Risk-free asset)이 존재한다는 것이다. 일반적으로 정부가 발행하는 국채를 무위험 자산으로 간주한다. 세번째 가정은, 모든 투자자들은 개별 자산의 수익성과 리스크, 즉 예상 수익률과 이러한 예상 수익률의 표준편차에 대하여 모두 같은 생각을 갖고 있다는 것이다.
     이러한 세 가지 가정으로부터 약간의 통계학 지식(Covariance: 공분산)과 약간의 수학적 지식(미분)을 이용해 논리를 전개하면, 위에 적혀있는 CAPM식과 베타의 정의를 도출해 낼 수 있다. CAPM식과 베타의 정의를 도출해 내는 과정은 대학원 과정에서 취급하기 때문에, Finance를 전공하는 학자가 될 것이 아니라면 굳이 신경쓸 필요는 없다. 그러나 그리 어려운 내용은 아니기 때문에 (다소 지루하겠지만), 궁금한 사람은 다음 논문을 보면 된다: “Capital Asset Prices: a Theory of Market Equilibrium under Conditions of Risk,” by William F. Sharpe, Journal of Finance, Vol. XIX, No.3, September 1964. CAPM에 대해 보다 포괄적이고 학문적인 설명을 원한다면, 영어로 쓰인 Wikipedia나 영어 원서 교재, 영문 Article을 참고하는 것이 좋다.

     일반적으로 학부 학생들이나 일반인들이 CAPM을 이해하는 데 있어 중요한 것은, 첫째, 세 가지 가정의 내용을 알아 두는 것이고, 둘째, CAPM의 핵심 메시지인
“적정 수익률/할인율 = 무위험 자산의 수익률 + 리스크 프리미엄
= 무위험 자산의 수익률 + 베타x (시장 전체의 예상 수익률 – 무위험 자산의 수익률)”을 이해하는 것이며, 셋째, 베타의 의미를 잘 이해해 두는 것이라 할 수 있다



출처 : http://sunho55.blogspot.kr/2014/10/capital-asset-pricing-model-capm-ii.html

저작자표시 비영리 변경금지

'鑑定評價理論 및 업역 확장 > 부동산 투자론' 카테고리의 다른 글

자본비용(Cost of Capital)과 Systematic Risk (체계적 위험)  (0) 2017.05.16
Capital Asset Pricing Model (CAPM): 베타(β: Beta)란? (III)개별 주식과 시장 전체의 연관성을 측정하는 지표다.  (0) 2017.05.14
Capital Asset Pricing Model (CAPM)이란? (I) (출처 : 최선호 교수 블로그)  (0) 2017.05.12
임대주택사업의 사업성 분석방법 개선에 관한 연구 (유선종 교수님 외)  (0) 2015.09.26
상권분석 방법론 (출처 : 이데일리)  (0) 2015.09.16

Capital Asset Pricing Model (CAPM)이란? (I)


Capital Asset Pricing Model (CAPM)이란? (I)
할인율(Discount Rate), 즉 자본비용을 계산하는 모델을 말한다.

우리말이 아닌 영어로 된 용어를 한번 듣고 대충 내용을 짐작하기는 쉽지 않은 경우가 많다. Capital Budgeting이나 Capital Asset Pricing Model(CAPM) 같은 것들이 좋은 예일 것이다. CAPM의 의미는 앞의 두 단어, 즉 Capital Asset을 빼고 뒤의 두 단어만 보면 보다 쉽게 이해할 수 있다.

 
CAPM은 Pricing Model이다.
     Capital Asset Pricing Model은 Pricing Model이다, 그러니까 Pricing, 즉 가격을 결정하는 데 사용하는 모델인 것이다. 그렇다면 무엇의 가격을 결정한다는 말인가? Asset, 즉 자산의 가격을 결정한다는 것이고, 자산 가운데서도 Capital Asset, 즉 장기 자산의 가격을 결정하는데 사용한다는 의미이다. 


     여기서 “Capital Asset”을 “자본 자산”이라고 번역하면, 우리말에서는 내용을 짐작하기 어려운, 어색한 용어가 되어 버린다. Capital은 자본인데, 일반적으로 자본이란 “장기간” 사용하는 자원이라는 의미를 갖고 있다. 자본이란 생산적 활동에 사용되는 자원(Resource)인데, 단기간에 쓸만 한 것을 생산해 내기는 어렵다. 무엇이든 쓸모 있는 것을 생산해 내기 위해서는 적지 않은 시간이 필요하기 때문에, 자본이라는 말에는 항상 적지 않은 시간 동안, 즉 장기적으로 사용한다는 의미가 내포되어 있다. 따라서 영어로 Capital Asset이란 우리말로는 “장기 자산”을 의미하는 것이다.



     이러한 Capital Asset, 즉 장기 자산의 대표적인 예는 주식이다. 주식은 채권과는 달리 만기가 없다. 만기가 없다는 것은 만기가 무한대라는 것과 같은 의미이기 때문에 가장 오랫동안 사용할 수 있는 자본이 된다. 그래서 주식이 장기 자산과 장기 자본의 대표적 예인 것이다. 이때 투자자의 입장에서는 장기 자산이 되고, 회사의 입장에서는 장기 자본이 된다.


     물론 Capital Asset이 주식만을 의미하는 것은 아니다. 이론적으로는, 주식뿐 아니라 채권, 부동산이나 귀금속 등 투자 포트폴리오 구성이 가능한 모든 자산이 포함된다. 그러나 현실적으로 모든 종류의 자산을 다 포괄하는 포트폴리오을 구성할 수도 없고 또 굳이 그렇게 할 필요도 없기 때문에, CAPM의 적용 대상이 되는 Capital Asset은 주로 주식이 된다.



CAPM은 Asset Price가 아니라 할인율을 계산하는 모델이다.


     Pricing Model이란 가격을 계산하는 모델을 말한다. 그렇지만 CAPM이 Capital Asset의 가격을 계산해 주지는 않는다. CAPM은 자산의 가격을 계산할 때 필요한 할인율(Discount Rate)만을 제공해 줄 뿐이다. 우리가 현재가치법(Present Value Method 또는 Discounted Cash Flow Method)을 이용해 자산 가격을 계산할 때, 먼저 자산이 창출해 낼 미래의 현금흐름을 추정하고, 이렇게 추정된 미래의 현금흐름을 현재 가치로 환산하는데, 이처럼 미래의 현금흐름을 현재 가치로 환산할 때 사용하는 할인율을 CAPM이 제공해 주는 것이다.


     할인율은 자산에 따라 달라진다. 예를 들어, 삼성전자 주식 가치를 계산하기 위해 사용하는 할인율과 현대자동차 주식에 적용하는 할인율이 다르고, 또 같은 업종 내에서도 삼성전자와 LG전자에 적용하는 할인율이 다르다. 이는 각각의 기업이 갖고 있는 사업의 특성과 이에 따른 위험 정도가 서로 다르기 때문이다. CAPM은 이러한 위험 수준을 고려해서 적절한 할인율을 계산해 내는 모델인 것이다.


     그런데 자산 가격을 산출하기 위해서는 할인율만 안다고 되는 것이 아니라, 미래의 현금흐름도 알아야 한다. 할인율을 책정하는 것도 어려운 일이지만, 미래의 현금흐름을 추정하는 것 또한 매우 어려운 일이다. 그러나 CAPM은 이 같은 미래의 현금흐름을 추정하는 데에는 전혀 쓸모가 없다. 그런 면에서는 CAPM의 Pricing Model이라는 표현이 좀 과장된 것이라 생각할 수도 있겠지만, 학문적으로 CAPM을 도출한 과정을 자세히 살펴 보면 이러한 표현이 타당한 것임을 알 수 있다. (이에 대한 자세한 논의는 다음 기회에 - - -)


     CAPM을 이용해 이론적으로 계산해 낸 할인율은 투자자들이 요구하는 수익률(Required Rate of Return)이고, 투자자들의 기회비용(Opportunity Cost)이며, 기업 입장에서는 자본비용(Cost of Capital)이다. 그러니까 CAPM은 자본비용을 이론적으로 계산할 수 있게 해 주는 중요한 모델인 것이다.



출처 : http://sunho55.blogspot.kr/2014/10/capital-asset-pricing-model-capm-i.html

저작자표시 비영리 변경금지

'鑑定評價理論 및 업역 확장 > 부동산 투자론' 카테고리의 다른 글

Capital Asset Pricing Model (CAPM): 베타(β: Beta)란? (III)개별 주식과 시장 전체의 연관성을 측정하는 지표다.  (0) 2017.05.14
Capital Asset Pricing Model (CAPM)이란? (II) (출처 : 최선호 교수 블로그)  (0) 2017.05.13
임대주택사업의 사업성 분석방법 개선에 관한 연구 (유선종 교수님 외)  (0) 2015.09.26
상권분석 방법론 (출처 : 이데일리)  (0) 2015.09.16
부동산 수익에 대한 인식과 실제간 간극 (행동경제학적 해석)  (0) 2014.05.29


국민임대주택의 사업성 분석체계에 관한 연구 2012 국토연구.pdf


국민임대주택의 사업성 분석체계에 관한 연구 2012 국토연구.pdf
2.02MB

'鑑定評價理論 및 업역 확장 > 부동산 투자론' 카테고리의 다른 글

Capital Asset Pricing Model (CAPM)이란? (II) (출처 : 최선호 교수 블로그)  (0) 2017.05.13
Capital Asset Pricing Model (CAPM)이란? (I) (출처 : 최선호 교수 블로그)  (0) 2017.05.12
상권분석 방법론 (출처 : 이데일리)  (0) 2015.09.16
부동산 수익에 대한 인식과 실제간 간극 (행동경제학적 해석)  (0) 2014.05.29
부동산 투자 위험 요소 (2013 감정평가사 연수 ppt 자료)  (0) 2014.05.19


[김영갑의 상권 칼럼] 올바른 상권분석 방법이란?

      

이데일리 | EFN창업팀 | 입력 2015.09.01 07:30 | 수정 2015.09.01 07:30


[이데일리 창업] 상권에 대한 관심이 높아지면서 어떻게 상권분석을 해야 하는지에 대한 질문도 많아지고 있다. 일단 상권분석을 하는 방법을 정하기 위해서 선행되어야 하는 일이 있다. 바로 목적을 정하는 일이다. 어떤 목적으로 상권분석을 하느냐에 따라서 방법론도 다르게 적용해야 하기 때문이다. 따라서 상권분석의 유형을 기준으로 상권분석의 목적을 살펴보도록 한다.



상권분석 어떤 목적으로 활용하고 있는가?



상권분석이 체계화되고 현장의 활용도가 높아지면서 다양한 분야로 확산되고 있다. 상권분석의 중요성이 가장 크게 부각되는 분야로 창업부문을 들 수 있다. 기존 점포의 경우 영업부진을 극복하기 위한 목적으로 상권분석을 활용할 수 있다. 그 외에도 컨설팅, 가맹점 유치, 부동산 투자, 정기적인 환경분석, 지역활성화를 위하여 상권분석이 활용되고 있다. 이러한 내용을 구체적으로 정리하면 <그림 1>과 같다.



<그림 1> 상권분석의 목적

출처 : 창업성공을 위한 상권분석(김영갑 저, 교문사)


상권분석 어떤 방법으로 해야 하나?

상권분석을 ‘상권분석시스템으로 하는 것’이라고 오해하는 경우가 많다. 컨설턴트 중에서도 상권분석시스템을 이용하여 상권의 현황을 파악하는 정도를 상권분석이라고 알고 있는 경우도 있다. 상권분석을 하는 방법은 매우 다양하다. <그림 2>에서 보는 바와 같이 크게 3가지 분류가 가능하고 세부적으로는 최소 9가지의 방법을 활용한다.



<그림 2> 상권분석 방법론

출처 : 창업성공을 위한 상권분석(김영갑 저, 교문사)


첫째, 정성적 분석법을 살펴본다.주관적 평가법이란 ‘경험이 많은 전문가의 의견을 중심으로 상권을 분석하는 방법’이다. 체크리스트법은 ‘상권에 영향을 주는 변수에 대한 평가표를 만들고 이를 활용하여 상권을 분석하는 방법’이다. 현황조사법은 ‘상권에 영향을 주는 변수에 대한 현황표를 만들고 이를 채워나가는 방법’이다.



둘째, 정량적 분석법은 설문조사법, 통계조사법, 수학적 방법이 있다.설문조사법은 ‘상권을 대표하는 표본을 대상으로 설문조사와 인터뷰를 통해 상권을 분석하는 방법’이다. 통계조사법은 ‘상권분석시스템에서 제공하는 상권관련 통계수치를 이용하는 방법’이다. 물론 시스템이 아닌 다른 출처의 통계수치를 활용하는 것을 포함한다. 수학적 방법은 ‘경험적 연구를통해 검증된 인과관계를 이용하여 회귀식과 같은 수학식을 개발하는 방법’을 의미한다. 외식업체에 누적된 통계자료와 수학식을 이용하여 원하는 결과값을 과학적으로 도출할 수 있다.



셋째, 소셜분석은 SNS에서 회자되는 내용을 이용하여 상권을 분석하는 방법으로 키워드분석, 추세분석, 내용분석, 분류 분석 등이 있다.키워드분석은 ‘포탈사이트의 키워드 현황, 키워드별 조회수 및 월별 추이, 연관키워드 현황에서 상권과 관련된 내용을 분석하는 방법’이다. 내용분석은 SNS의 내용을 월별, 방문목적, 동반자, 음식점 브랜드, 방문시간, 구매 메뉴, 만족도 및 구체적 의견 등에서 상권과 관련된 내용을 분석하는 방법‘이다. 추세분석(트랜드분석)은 포탈사이트의 키워드 검색수를 시계열로 분석하여 미래를 예측하는 방법’이다. 분류분석은 SNS의 내용을 상권과 관련된 내용을 감성언어 및 긍/부정을 기준으로 분류하여 분석하는 방법‘을 뜻한다.



실제로 현장에서 상권분석을 할 때는 특정한 분석법을 집중적으로 사용하기 보다는 9가지 방법을 종합적, 유기적으로 활용하여 분석하는 것이 권장된다. 특히 자신의 분석 목적에 따라서 어떤 방법론이 가장 적합한지에 대한 나름의 실증이 필요하다.



상권정보시스템 어떻게 활용해야 좋을까?



다양한 상권분석 방법이 존재함에도 불구하고 편의상 상권정보시스템(또는 상권분석시스템)을 주로 이용하는 경우가 많다. 이는 통계적 분석법의 일환으로 개발된 상권정보시스템이 누구나 쉽게 사용할 수 있게 설계되었다는 점과 현황이 일목요연하게 정리가 되어 있기 때문이라고 볼 수 있다. 무엇보다도 가장 큰 매력은 무료로 사용이 가능하다는 점이다. 물론 유료 서비스도 존재한다.



그런데 상권분석이 편의성에만 목표를 두고 이루어진다면 결과가 어떻게 나타나겠는가? 상권분석을 하는 과정에서 분석자가 유의해야 할 내용과 상권분석의 지향점을 살펴보면 다음과 같다.



첫째, 많은 상권정보시스템이 상권의 현황을 보여주기는 하지만 구체적으로 어떤 행동을 해야 하는지 알려주지 못하고 있다.예를 들면 매출이 낮은 사업자가 열심히 지역과 업종을 선택하고 분석 버튼을 눌러도 어떤 행동을 해야 매출이 올라가는지 알려주는 시스템은 찾기가 어렵다. 구체적으로는 상권의 평균매출액과 타 상권의 평균매출액을 비교하여 매출이 더 높은 상권을 보여주는 수준에 그친다.




둘째, 창업자가 특정지역에서 업종을 선택하면, 밀집도가 높으니 창업을 조심하라는 행동 방침을 알려주는 경우도 있다.하지만 밀집도가 높으면 위험하고, 밀집도가 낮으면 유리하다고 단언하기 힘들다. 전략적 측면에서 보면 동일업종의 밀집도가 높은 경우 소비자의 유입력이 더 커지는 경우가 비일비재하다. 즉 상권은 획일적인 단일 변수로 설명이 어려운 경우가 많다는 점을 상기해야 한다.




셋째, 상권정보시스템에서 어떤 지역을 선택했을 때, 창업을 하면 좋을 업종을 추천하고 특정 브랜드까지 추천하는 서비스가 존재한다.그런데 이 서비스는 창업자가 창업을 위해 지출한 투자금을 상회하는 이익이 가능한지는 알려주지 못한다. 우리가 상권분석시스템을 통해 알고 싶은 것은 투자수익율이 어느 정도 되는지에 대한 정보이다. 즉 창업자가 지불하게 될 비용을 상회하는 이익의 여부가 중요한 결과이다



상권분석은 단순히 통계를 집계하여 정리하고 보여주는 수준에 그쳐서는 곤란하다. 어떤 활동을 해야 원하는 매출액과 이익을 얻을 수 있는지, 그 활동은 실제로 사업자가 직접 실천 가능한 것인지, 만약 실천이 가능하다면 비용 또는 투자 대비 이익은 얼마나 되는지를 알 수 있어야 한다.




물론 단기적으로 이런 상권분석방법의 완성을 기대하기는 어려워 보인다. 그럼에도 불구하고 이런 비전을 가지고 상권분석을 바라보는 자세는 항상 견지해야 한다. 그래야 중장기적으로 성과가 나타나지 않을까.



한양사이버대학교 호텔관광외식경영학과 교수 김영갑


(블로그 http://webkim.blog.me)


EFN창업팀 (startbiz@edaily.co.kr)


'鑑定評價理論 및 업역 확장 > 부동산 투자론' 카테고리의 다른 글

Capital Asset Pricing Model (CAPM)이란? (I) (출처 : 최선호 교수 블로그)  (0) 2017.05.12
임대주택사업의 사업성 분석방법 개선에 관한 연구 (유선종 교수님 외)  (0) 2015.09.26
부동산 수익에 대한 인식과 실제간 간극 (행동경제학적 해석)  (0) 2014.05.29
부동산 투자 위험 요소 (2013 감정평가사 연수 ppt 자료)  (0) 2014.05.19
시장타당성 분석 사례 보고서   (0) 2013.11.11

 

부동산 수익에 대한 인식과 실제간 간극 (행동경제학).pdf

부동산 수익에 대한 인식과 실제간 간극 (행동경제학).pdf
1.07MB
저작자표시 비영리 변경금지

'鑑定評價理論 및 업역 확장 > 부동산 투자론' 카테고리의 다른 글

임대주택사업의 사업성 분석방법 개선에 관한 연구 (유선종 교수님 외)  (0) 2015.09.26
상권분석 방법론 (출처 : 이데일리)  (0) 2015.09.16
부동산 투자 위험 요소 (2013 감정평가사 연수 ppt 자료)  (0) 2014.05.19
시장타당성 분석 사례 보고서   (0) 2013.11.11
부동산 투자회사법 일부개정 (2013.7.16 시행 2014.7.17)  (0) 2013.07.23

저작자표시 비영리 변경금지

'鑑定評價理論 및 업역 확장 > 부동산 투자론' 카테고리의 다른 글

상권분석 방법론 (출처 : 이데일리)  (0) 2015.09.16
부동산 수익에 대한 인식과 실제간 간극 (행동경제학적 해석)  (0) 2014.05.29
시장타당성 분석 사례 보고서   (0) 2013.11.11
부동산 투자회사법 일부개정 (2013.7.16 시행 2014.7.17)  (0) 2013.07.23
재투자수익률 가정 (음양화평지인)  (0) 2013.04.17

시장타당성분석사례.hwp

시장타당성분석사례.hwp
0.27MB
저작자표시 비영리 변경금지

'鑑定評價理論 및 업역 확장 > 부동산 투자론' 카테고리의 다른 글

상권분석 방법론 (출처 : 이데일리)  (0) 2015.09.16
부동산 수익에 대한 인식과 실제간 간극 (행동경제학적 해석)  (0) 2014.05.29
부동산 투자 위험 요소 (2013 감정평가사 연수 ppt 자료)  (0) 2014.05.19
부동산 투자회사법 일부개정 (2013.7.16 시행 2014.7.17)  (0) 2013.07.23
재투자수익률 가정 (음양화평지인)  (0) 2013.04.17

 

 

 

 

 

 

저작자표시 비영리 변경금지

'鑑定評價理論 및 업역 확장 > 부동산 투자론' 카테고리의 다른 글

상권분석 방법론 (출처 : 이데일리)  (0) 2015.09.16
부동산 수익에 대한 인식과 실제간 간극 (행동경제학적 해석)  (0) 2014.05.29
부동산 투자 위험 요소 (2013 감정평가사 연수 ppt 자료)  (0) 2014.05.19
시장타당성 분석 사례 보고서   (0) 2013.11.11
재투자수익률 가정 (음양화평지인)  (0) 2013.04.17

+ Recent posts

티스토리툴바